Advertisements
Advertisements
प्रश्न
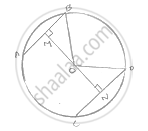
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
उत्तर
Draw OM ⊥ AB and ON ⊥ CD. Join OB and OD
`BM=(AB)/2=5/2`
`ND=(CD)/2=5/2`
Let ON be x , so OM will be 6-x in Δ MOB
`OM^2+MB^2=OB^2`
`(6-x)^2+(5/2)^2=OB^2`
`36+x^2-12x+25/4=OB^2`
In Δ NOD
`ON^2+ND^2=OD^2`
`x^2+(11/2)^2=OD^2`
`x^2+121/4=OD^2`
We have OB = OD. (radii of same circle)
So, from equation (1) and (2).
`36+x^2-12x+25/4=x^2+121/4`
`⇒12x=36+25/4-121/34`
`=(144+25-121)/4=48/4=12`
`x=1`
From equation (2)
`(1)^2+(121/4)=OD^2`
`OD^2=1+121/4=121/4`
`OD=(5sqrt5)/2`
So, radius of circle is found to be `(5sqrt5)/2cm`
APPEARS IN
संबंधित प्रश्न
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
true or false
If a circle is divided into three equal arcs each is a major arc.
true or false
A circle has only finite number of equal chords.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
