Question

Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.

पर्याय

• True

• False

Answer 1

This statement is True.

Explanation:

Let the congruent circles with centers O and O’ intersect at A and B.

Join AB, O’A, O’B, OA and OB.

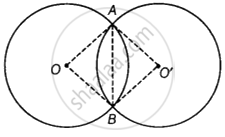
By joining the points, we obtain two triangles, namely OAB and O’AB.

Since both the circles are congruent, therefore in ΔOAB and ΔO’AB, we have:

OA = O’A   ...(Both circles have same radius as the circles are congruent)

OB = O’B  ...(Both circles have same radius as the circles are congruent)

AB = AB  ...(Common)

∴ By SSS congruence rule, ΔOAB = ΔO’AB

∴ By CPCT, ∠AOB = ∠AO’B