Advertisements
Advertisements
प्रश्न
Prove that two different circles cannot intersect each other at more than two points.
उत्तर
Suppose two circles intersect in three points A,B,C,
Then A,B,C are non-collinear. So, a unique circle passes through these three points. This is contradiction to the face that two given circles are passing through A,B,C. Hence, two circles cannot intersect each other at more than two points.
APPEARS IN
संबंधित प्रश्न
Prove that the tangents at the extremities of any chord make equal angles with the chord.
ture or false v
The degree measure of a semi-circle is 180°.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

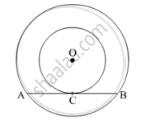
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
Number of circles that can be drawn through three non-collinear points is
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
If O is the centre of the circle, find the value of x in each of the following figures

Use the figure given below to fill in the blank:
Diameter = 2 x ________

Find the diameter of the circle
Radius = 6 cm
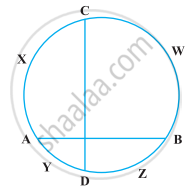
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.