Advertisements
Advertisements
प्रश्न
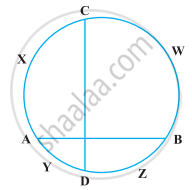
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
उत्तर
Given: In a circle AYDZBWCX, two chords AB and CD intersect at right angles.
To prove: arc CXA + arc DZB = arc AYD + arc BWC = Semi-circle.
Construction: Draw a diameter EF parallel to CD having centre M.
Proof: Since, CD || EF
arc EC = arc PD ...(i)
arc ECXA = arc EWB [Symmetrical about diameter of a circle]
arc AF = arc BF ...(ii)
We know that, ar ECXAYDF = Semi-circle
arc EA + arc AF = Semi-circle
⇒ arc EC + arc CXA = arc FB = Semi-circle ...[From equation (ii)]
⇒ arc DF + arc CXA + arc FB = Semi-circle ...[From equation (i)]
⇒ arc DF + arc FB + arc CXA = Semi-circle
⇒ arc DZB + arc C × A = Semi-circle
We know that, circle divides itself in two semi-circles, therefore the remaining portion of the circle is also equal to the semi-circle.
∴ arc AYD + arc BWC = Semi-circle
Hence proved.
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
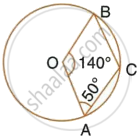
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.
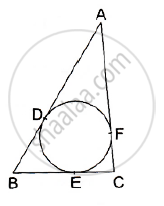
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
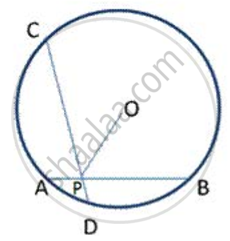
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.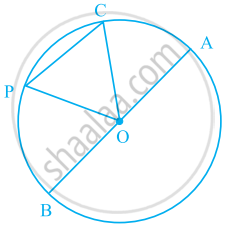
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
