Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

उत्तर

Here,
=
= 110°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Now, OA = OB (Radii of same circle)
∴ ∠OBA = ∠OAB
=
= 20°
∴ ∠CAB = 50° – 20° = 30°
ΔCAB,
∠CBA = 180° – 110° – 30° = 40°
∴ ∠OBC = ∠CBA + ∠OBA
= 40° + 20°
= 60°
APPEARS IN
संबंधित प्रश्न
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, PO

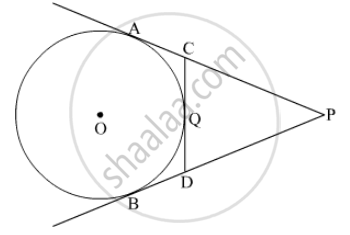
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Draw circle with the radii given below.
3 cm
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
Find the radius of the circle
Diameter = 24 cm
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
In the given figure, O is the centre of the circle. Name all chords of the circle.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
