Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

Solution

Here, `∠ACB = 1/2 "Reflex" (∠AOB)`
= `1/2 (360^circ - 140^circ)`
= 110°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Now, OA = OB (Radii of same circle)
∴ ∠OBA = ∠OAB
= `(180^circ - 140^circ)/2`
= 20°
∴ ∠CAB = 50° – 20° = 30°
ΔCAB,
∠CBA = 180° – 110° – 30° = 40°
∴ ∠OBC = ∠CBA + ∠OBA
= 40° + 20°
= 60°
APPEARS IN
RELATED QUESTIONS
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Fill in the blank
A continuous piece of a circle is ............... of the circle
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.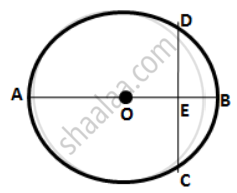
Draw circle with the radii given below.
3 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

