Advertisements
Advertisements
Question
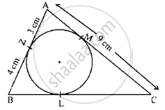
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

Solution
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore, we have
BQ = BP
Let us denote BP and BQ by x
AP = AR
Let us denote AP and AR by y
RC = QC
Let us denote RC and RQ by z
We have been given that ΔABC is a right triangle and BC = 6 cm and AB = 8 cm. let us find out AC using Pythagoras theorem. We have,
`AC^2=AB^2+BC^2`
`AC^2=6^2+8^2`
`AC^2=36+64`
`AC^2=100`
`AC= sqrt100`
`AC=10`
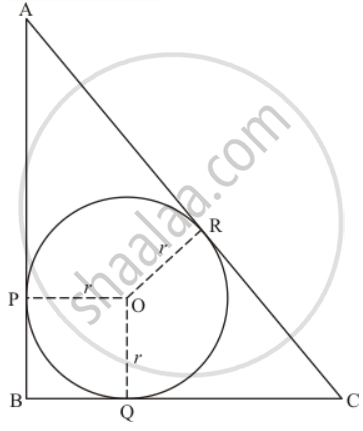
Consider the perimeter of the given triangle. We have,
AB + BC + AC = 8 + 6 + 10
AB + BC + AC = 24
Looking at the figure, we can rewrite it as,
AP + PB + BQ + QC + AR + RC = 24
Let us replace the sides with the respective x, y and z which we have decided to use.
`y+x+x+z+y+z=24`
`2x+2y+2z=24`
`2(x+y+z)=24`
`x+y+z=12`
Now, consider the side AC of the triangle.
AC = 10
Looking at the figure we can say,
AR + RC = 10
y + z = 10 …… (2)
Now let us subtract equation (2) from equation (1). We have,
x + y + z = 12
y + z = 10
After subtracting we get,
x = 2
That is,
BQ = 2, and
BP = 2
Now consider the quadrilateral BPOQ. We have,
BP = BQ (since length of two tangents drawn to a circle from the same external point are equal)
Also,
PO = OQ (radii of the same circle)
It is given that `∠PBQ= 90^o`
From the property of tangents, we know that the tangent will be at right angle to the radius of the circle at the point of contact. Therefore,
`∠OPB= 90^o`
`∠OQB= 90^o`
We know that sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠PBQ+∠OPB+∠OQB+∠POQ=360^o`
`90^o + 90^o +90^o + ∠POQ= 360^o`
`270^o + ∠POQ = 360^o`
`∠ POQ= 90^o`
Since all the angles of the quadrilateral are equal to `90^o`and the adjacent sides also equal, this quadrilateral is a square. Therefore, all sides will be equal. We have found out that,
BP = 2 cm
Therefore, the radii
PO = 2 cm
Thus the radius of the incircle of the triangle is 2 cm.
APPEARS IN
RELATED QUESTIONS
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
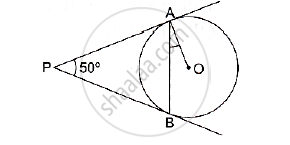
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.
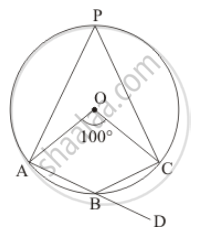
In the given figure, O is the centre of the circle. Find ∠CBD.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is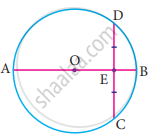
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______