Question

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

Answer 1

From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore, we have

BQ = BP

Let us denote BP and BQ by x

AP = AR

Let us denote AP and AR by y

RC = QC

Let us denote RC and RQ by z

 

We have been given that _ΔABC  is a right triangle and BC = 6 cm and AB = 8 cm. let us find out AC using Pythagoras theorem. We have,

`AC^2=AB^2+BC^2`

`AC^2=6^2+8^2`

`AC^2=36+64`

`AC^2=100`

`AC= sqrt100`

`AC=10`

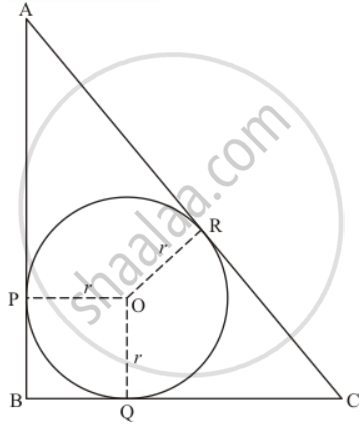
Consider the perimeter of the given triangle. We have,

AB + BC + AC = 8 + 6 + 10

AB + BC + AC = 24

Looking at the figure, we can rewrite it as,

AP + PB + BQ + QC + AR + RC = 24

Let us replace the sides with the respective x, y and z which we have decided to use.

`y+x+x+z+y+z=24`

`2x+2y+2z=24`

`2(x+y+z)=24`

`x+y+z=12`

Now, consider the side AC of the triangle.

AC = 10

Looking at the figure we can say,

AR + RC = 10

y + z = 10 …… (2)

Now let us subtract equation (2) from equation (1). We have,

x + y + z = 12

y + z = 10

After subtracting we get,

x = 2

That is,

BQ = 2, and

BP = 2

Now consider the quadrilateral BPOQ. We have,

BP = BQ (since length of two tangents drawn to a circle from the same external point are equal)

Also,

PO = OQ (radii of the same circle)

It is given that `∠PBQ= 90^o` 

From the property of tangents, we know that the tangent will be at right angle to the radius of the circle at the point of contact. Therefore,

`∠OPB= 90^o` 

`∠OQB= 90^o` 

We know that sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,

`∠PBQ+∠OPB+∠OQB+∠POQ=360^o`

`90^o + 90^o +90^o + ∠POQ= 360^o`

`270^o + ∠POQ = 360^o`

`∠ POQ= 90^o`

Since all the angles of the quadrilateral are equal to `90^o`and the adjacent sides also equal, this quadrilateral is a square. Therefore, all sides will be equal. We have found out that,

BP = 2 cm

Therefore, the radii

PO = 2 cm

Thus the radius of the incircle of the triangle is 2 cm.