Advertisements
Advertisements
प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
योग
उत्तर
Let O be the centre of the given circle and let P be a point such that OP = 10 cm.
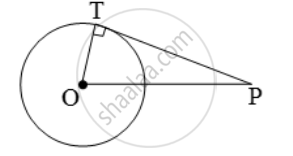
Let PT be the tangent such that PT = 8 cm.
Join OT.
Now, PT is a tangent at T and OT is the radius through T.
∴ OT ⊥ PT.
In the right ∆OTP, we have
`OP^2 = OT^2 + PT^2 ` [by Pythagoras’ theorem]
`\RightarrowOT=\sqrt{OP^{2}-PT^{2}}=\sqrt{(10)^{2}-(8)^{2})\text{ cm}`
= √36 cm = 6 cm.
Hence, the radius of the circle is 6 cm
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
