Question

From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.

Answer 1

Let O be the centre of the given circle and let P be a point such that OP = 10 cm.

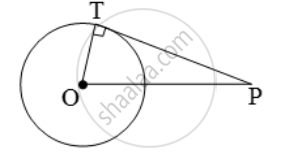
Let PT be the tangent such that PT = 8 cm.

Join OT.

Now, PT is a tangent at T and OT is the radius through T.

∴ OT ⊥ PT.

In the right ∆OTP, we have

`OP^2 = OT^2 + PT^2 ` [by Pythagoras’ theorem]

`\RightarrowOT=\sqrt{OP^{2}-PT^{2}}=\sqrt{(10)^{2}-(8)^{2})\text{ cm}`

= √36 cm = 6 cm.

Hence, the radius of the circle is 6 cm