Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

उत्तर
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore, we have
BQ = BP
Let us denote BP and BQ by x
AP = AR
Let us denote AP and AR by y
RC = QC
Let us denote RC and RQ by z
We have been given that ΔABC is a right triangle and BC = 6 cm and AB = 8 cm. let us find out AC using Pythagoras theorem. We have,
`AC^2=AB^2+BC^2`
`AC^2=6^2+8^2`
`AC^2=36+64`
`AC^2=100`
`AC= sqrt100`
`AC=10`
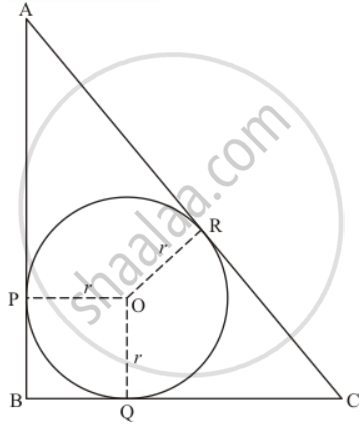
Consider the perimeter of the given triangle. We have,
AB + BC + AC = 8 + 6 + 10
AB + BC + AC = 24
Looking at the figure, we can rewrite it as,
AP + PB + BQ + QC + AR + RC = 24
Let us replace the sides with the respective x, y and z which we have decided to use.
`y+x+x+z+y+z=24`
`2x+2y+2z=24`
`2(x+y+z)=24`
`x+y+z=12`
Now, consider the side AC of the triangle.
AC = 10
Looking at the figure we can say,
AR + RC = 10
y + z = 10 …… (2)
Now let us subtract equation (2) from equation (1). We have,
x + y + z = 12
y + z = 10
After subtracting we get,
x = 2
That is,
BQ = 2, and
BP = 2
Now consider the quadrilateral BPOQ. We have,
BP = BQ (since length of two tangents drawn to a circle from the same external point are equal)
Also,
PO = OQ (radii of the same circle)
It is given that `∠PBQ= 90^o`
From the property of tangents, we know that the tangent will be at right angle to the radius of the circle at the point of contact. Therefore,
`∠OPB= 90^o`
`∠OQB= 90^o`
We know that sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠PBQ+∠OPB+∠OQB+∠POQ=360^o`
`90^o + 90^o +90^o + ∠POQ= 360^o`
`270^o + ∠POQ = 360^o`
`∠ POQ= 90^o`
Since all the angles of the quadrilateral are equal to `90^o`and the adjacent sides also equal, this quadrilateral is a square. Therefore, all sides will be equal. We have found out that,
BP = 2 cm
Therefore, the radii
PO = 2 cm
Thus the radius of the incircle of the triangle is 2 cm.
APPEARS IN
संबंधित प्रश्न
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

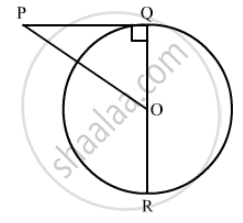
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
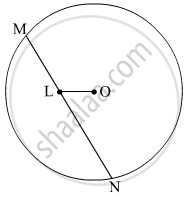
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Can the length of a chord of a circle be greater than its diameter ? Explain.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
