Advertisements
Advertisements
प्रश्न
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
पर्याय
2 : 3
1 : 4
4 : 1
1 : 3
उत्तर
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is 1 : 4.
Explanation:
An arc that subtends an angle of 90° at the center of a circle represents a quarter of the full circle because a full circle has 360°
`= (90°)/(360°) = 1/4`
Therefore, the ratio of the arc length to the circumference of the circle is 1 : 4
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
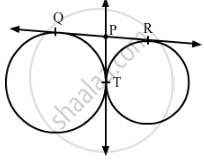
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
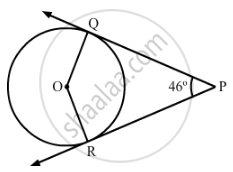
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Can the length of a chord of a circle be greater than its diameter ? Explain.
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
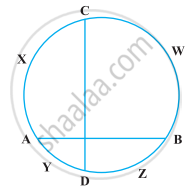
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.