Advertisements
Advertisements
प्रश्न
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
पर्याय
- \[\sqrt{5} \] cm
- \[2\sqrt{5}\] cm
\[2\sqrt{7} \] cm
- \[\sqrt{7}\] cm
उत्तर
We will represent the given data in the figure
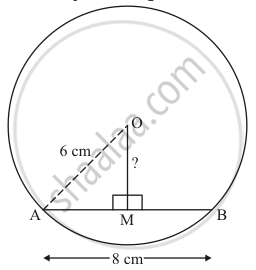
We know that perpendicular drawn from the centre to the chord divides the chord into two equal parts.
So , AM = MB = \[\frac{AB}{2} = \frac{8}{2}\] = 4 cm.
Using Pythagoras theorem in the ΔAMO,
`OM^2 = AO^2 - AM^2`
`= 6^2 - 4^2`
= 36-16
`= sqrt(20)`
= `2sqrt(5)` cm
APPEARS IN
संबंधित प्रश्न
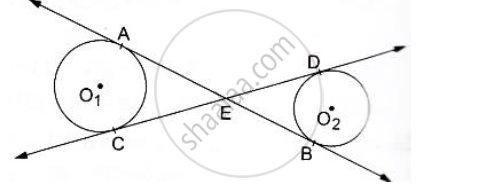
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
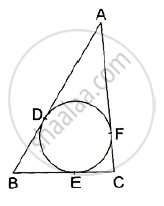
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?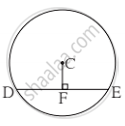
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.