Advertisements
Advertisements
प्रश्न
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
विकल्प
- \[\sqrt{5} \] cm
- \[2\sqrt{5}\] cm
\[2\sqrt{7} \] cm
- \[\sqrt{7}\] cm
उत्तर
We will represent the given data in the figure
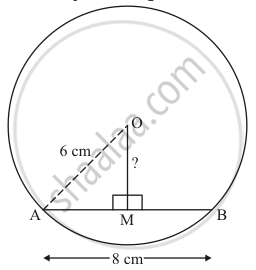
We know that perpendicular drawn from the centre to the chord divides the chord into two equal parts.
So , AM = MB = \[\frac{AB}{2} = \frac{8}{2}\] = 4 cm.
Using Pythagoras theorem in the ΔAMO,
`OM^2 = AO^2 - AM^2`
`= 6^2 - 4^2`
= 36-16
`= sqrt(20)`
= `2sqrt(5)` cm
APPEARS IN
संबंधित प्रश्न
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Can the length of a chord of a circle be greater than its diameter ? Explain.
Draw circle with the radii given below.
3 cm
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
What is the area of a semi-circle of diameter ‘d’?
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
