Advertisements
Advertisements
प्रश्न
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
विकल्प
15 cm
16 cm
17 cm
34 cm
उत्तर
17 cm
We will represent the given data in the figure
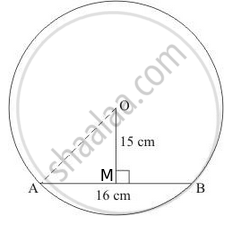
In the diagram AB is the given chord of 16 cm length and OM is the perpendicular distance from the centre to AB.
We know that perpendicular from the centre to any chord divides it into two equal parts.
So, AM = MB = `16/2` = 8 cm.
Now consider right triangle OMA and by using Pythagoras theorem
`AO^2 = AM^2 + OM^2`
`= 8^2 + 15^2`
= 64+225
= 289
`= sqrt(289)`
= 17 cm
APPEARS IN
संबंधित प्रश्न
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Prove that the tangents at the extremities of any chord make equal angles with the chord.
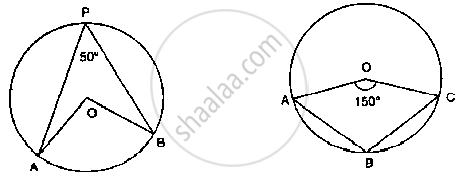
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
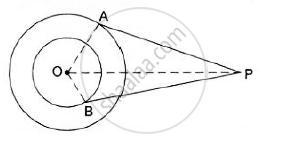
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

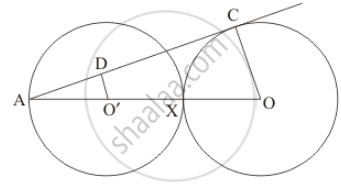
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
The circle which passes through all the vertices of a triangle is called ______.
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c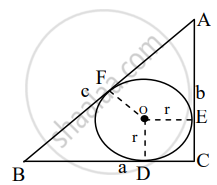
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
