Advertisements
Advertisements
प्रश्न
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

विकल्प
A. 55°
B. 70°
C. 45°
D. 35°
उत्तर
In ΔOPQ:
OP = OQ (Radii of same circle)
⇒ ∠OQP = ∠OPQ (Equal sides have equal angles opposite to them)
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of triangles)
⇒ 70° + 2∠OPQ = 180°
⇒ 2∠OPQ = 180° − 70° = 110°
⇒ ∠OPQ = 55°
It is known that the tangent is perpendicular to the radius through the point of contact.
∴ ∠OPT = 90°
⇒ ∠OPQ + ∠TPQ = 90°
⇒ 55° + ∠TPQ = 90°
⇒ ∠TPQ = 90° − 55° = 35°
The correct answer is D.
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
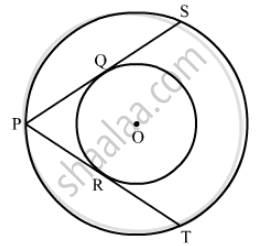
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
Is every diameter of a circle also a chord?
