Advertisements
Advertisements
प्रश्न
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
विकल्प
60°
45°
30°
15°
उत्तर
We will associate the given information in the following figure.
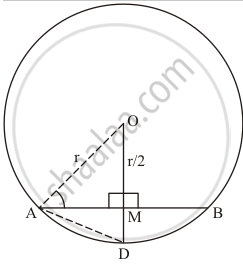
Since AO = r (radius of circle)
AM = `r/2` (given)
Extended OM to D where MD = `r/2`
Consider the triangles AOM and triangle AMD
OM = MD
`angleAMO = angle AMD` = 90°
AM = AM (common Sides
So by SSS property
Δ AMO ≅ Δ DM
So AD = AO = r and OD=OM+MD=r
Hence ΔAOD is equilateral triangle
So `angle OAD` = 60°
We know that in equilateral triangle altitudes divide the vertex angles
Therefore `angleOAM = (angleOAD)/2`
`=60/2`
= 30°
APPEARS IN
संबंधित प्रश्न
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
