Advertisements
Advertisements
प्रश्न
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
उत्तर
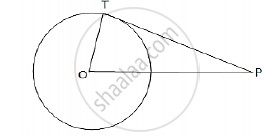
Let O be the center of the given circle.
Let P be a point, such that
OP = 17 cm.
Let OT be the radius, where
OT = 5cm
Join TP, where TP is a tangent.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`TP = sqrt(OP^2 - OT^2)`
`=sqrt(17^2 -8^2)`
` =sqrt(289-64)`
`= sqrt(225)`
= 15 cm
∴ The length of the tangent is 15 cm.
APPEARS IN
संबंधित प्रश्न
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
The longest chord of a circle is __________
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
