Advertisements
Advertisements
प्रश्न
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
उत्तर
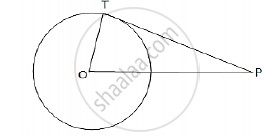
Let O be the center of the given circle.
Let P be a point, such that
OP = 17 cm.
Let OT be the radius, where
OT = 5cm
Join TP, where TP is a tangent.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`TP = sqrt(OP^2 - OT^2)`
`=sqrt(17^2 -8^2)`
` =sqrt(289-64)`
`= sqrt(225)`
= 15 cm
∴ The length of the tangent is 15 cm.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
From the figure, identify a sector.

