Advertisements
Advertisements
प्रश्न
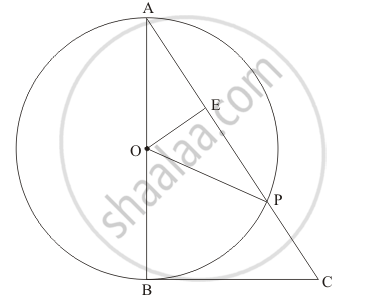
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
उत्तर
Given: AB = 10 units, AC = 6 units, PC = PQ = x unit.
To find: x
Solution:
Diameter AB = 10 ...[Given]
∴ Radius = `1/2 xx "AB" = 1/2 xx 10` = 5.
∴ OQ = AO = OB = 5 ......(i)
AC = AO + OC .....[A–O–C]
∴ OC = AC – AO
∴ OC = 6 – 5 ......[Given and (i)]
∴ OC = 1 ......(ii)
OQ = OP + PQ ......[O–P–Q]
∴ OP = OQ – PQ
= 5 – x ......(iii) [From (i) and given]
Note that seg AB is tangent to the given smaller circle at point C.
∴ ∠PCO = 90° ......[Tangent theorem]
∴ In ∆PCO,
∠PCO = 90°
∴ OP2 = PC2 + OC2 ......[Pythagoras theorem]
∴ (5 – x)2 = x2 + (1)2 ......[From (ii) and (iii)]
∴ 25 – 10x + x2 = x2 + 1
∴ 10x = 24
∴ x = `24/10` = 2.4
∴ The radius x of the smaller circle is 2.4 units
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
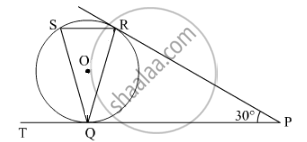
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
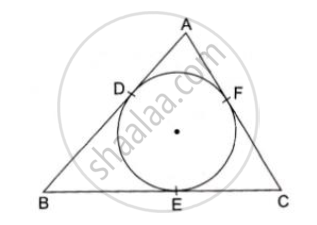
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
A line segment which joins any two points on a circle is a ___________
The ______________ is the longest chord of a circle
Find the radius of the circle
Diameter = 76 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.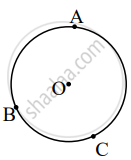
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
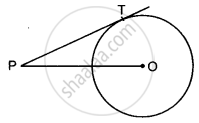
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Is every diameter of a circle also a chord?
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
