Advertisements
Advertisements
प्रश्न
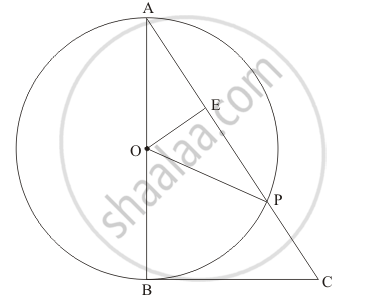
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
उत्तर
The figure given in the question is below
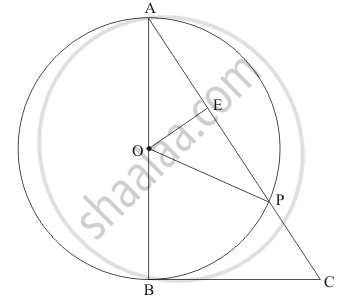
Let us first take up Δ AOP.
We have,
OA = OP (Since they are the radii of the same circle)
Therefore, Δ AOP. is an isosceles triangle. From the property of isosceles triangle, we know that, when a median drawn to the unequal side of the triangle will be perpendicular to the unequal side. Therefore,
`∠ OEA=90^o`
Now let us take up Δ AOE and Δ ABC..
We know that the radius of the circle will always be perpendicular to the tangent at the point of contact. In this problem, OB is the radius and BC is the tangent and B is the point of contact. Therefore,
`∠ ABC=90^o`
Also, from the property of isosceles triangle we have found that
`∠ OEA = 90^o`
Therefore,
`∠ ABC`= `∠ OEA`
`∠ A` is the common angle to both the triangles.
Therefore, from AA postulate of similar triangles,
`ΔAOE` ~ `ΔABC`
Thus we have proved.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
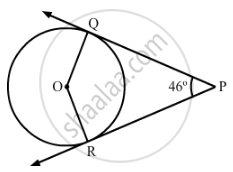
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

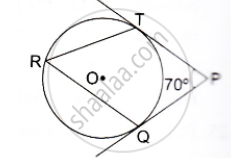
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
The circle which passes through all the vertices of a triangle is called ______.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
The ratio between the circumference and diameter of any circle is _______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
What is the area of a semi-circle of diameter ‘d’?
