Advertisements
Advertisements
प्रश्न
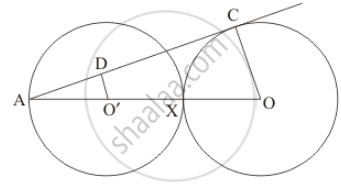
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
उत्तर
Consider the two triangles Δ ADOand Δ ACO.

We have,
∠ A is a common angle for both the triangles.
`∠ ADO =90^o` (Given in the problem)
`∠ ACO = 90^o` (Since OC is the radius and AC is the tangent to that circle at C and we know that the radius is always perpendicular to the tangent at the point of contact)
Therefore,
`∠ ADO = ∠ACO`
From AA similarity postulate we can say that,
Δ ACO ~ Δ ADO
Since the triangles are similar, all sides of one triangle will be in same proportion to the corresponding sides of the other triangle.
Consider AO′ of Δ ADO and AO of Δ ACO .
`(AO)/(AO)=(AO)/(AO+OX+OX)`
Since AO′ and O′X are the radii of the same circle, we have,
AO′ = O′X
Also, since the two circles are equal, the radii of the two circles will be equal. Therefore,
AO′ = XO
Therefore we have
`(AO)/(AO)=(AO)/(AO+AO+AO)`
`(AO)/(AO)=1/3`
Since Δ ACO ~ Δ ADO,
`(AO)/(AO)=(DO)/(CO)`
We have found that,
`(AO)/(AO)=1/3`
Therefore,
`(DO)/(CO)=1/3`
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
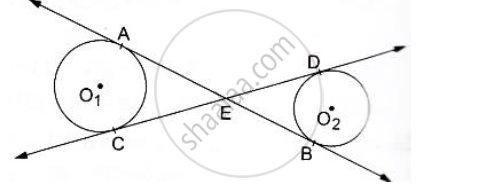
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

State, if the following statement is true or false:
The longest chord of a circle is its diameter.
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
