Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

उत्तर
It is given that, O is the centre of the circle and \[\angle DAB = 50° \]
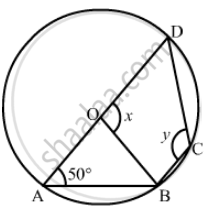
We have to find the values of x and y.
ABCD is a cyclic quadrilateral and `angle A + angle C = 180°`
So,
50° + y = 180°
y = 180° − 50°
y = 130°
Clearly Δ OAB is an isosceles triangle with OA = OB and `angle OBA = angle OAB`
Then, `angle OBA + angleOAB + angle AOB = 180°`
`angleAOB = 180° - ( 50° + 50° ) ` (Since `angleOBA = angle OAB = 50°` )
So, `angleAOB = 80°`
x + `angle AOB ` = 180° (Linear pair)
Therefore, x = 180° − 80° = 100°
Hence,
x = 100° and y = 130°
APPEARS IN
संबंधित प्रश्न
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
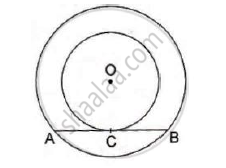
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
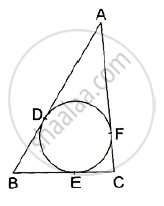
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
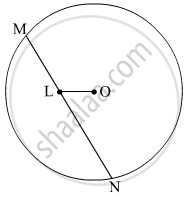
Use the figure given below to fill in the blank:
R is the _______ of the circle.

The radius of a circle of diameter 24 cm is _______
