Advertisements
Advertisements
प्रश्न
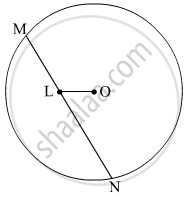
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
उत्तर
seg MN is a chord of a circle with centre O.
Draw OP ⊥ MN and join OM.

MP = PN = `(MN)/2 = 25/2`units (Perpendicular drawn from the centre of a circle on its chord bisects the chord)
∴ LP = MP − ML = `25/2-9=7/2`units
In right ∆OPL,
\[{OL}^2 = {LP}^2 + {OP}^2 \]
\[ \Rightarrow OP = \sqrt{{OL}^2 - {LP}^2}\]
\[ \Rightarrow OP = \sqrt{5^2 - \left( \frac{7}{2} \right)^2}\]
\[ \Rightarrow OP = \sqrt{25 - \frac{49}{4}}\]
\[ \Rightarrow OP = \sqrt{\frac{51}{4}} = \frac{1}{2}\sqrt{51} \] units
In right ∆OPM,
\[{OM}^2 = {MP}^2 + {OP}^2 \]
\[ \Rightarrow OM = \sqrt{\left( \frac{25}{2} \right)^2 + \left( \frac{\sqrt{51}}{2} \right)^2}\]
\[ \Rightarrow OM = \sqrt{\frac{625 + 51}{4}}\]
\[ \Rightarrow OM = \sqrt{\frac{676}{4}}\]
\[ \Rightarrow OM = \sqrt{169} = 13 \] units
Thus, the radius of the circle is 13 units.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

Prove that the tangents at the extremities of any chord make equal angles with the chord.
true or false
A circle is a plane figure.
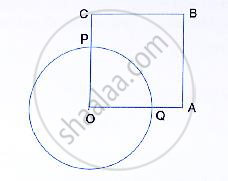
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

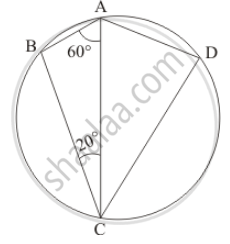
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
The ratio between the circumference and diameter of any circle is _______
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a diameter.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
