Advertisements
Online Mock Tests
Chapters
Advertisements
Solutions for Chapter 3: Circle
Below listed, you can find solutions for Chapter 3 of Maharashtra State Board Balbharati for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board.
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Practice Set 3.1 [Page 55]
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
- What is the length of each tangent segment?
- What is the measure of ∠MRO?
- What is the measure of ∠MRN?

Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Practice Set 3.2 [Page 58]
Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
If radii of two circles are 4 cm and 2.8 cm. Draw a figure of this circles touching each other externally.
If radii of two circles are 4 cm and 2.8 cm. Draw a figure of this circles touching each other internally.
In the given figure, the circles with centres P and Q touch each other at R. A line passing through R meets the circles at A and B respectively. Prove that – (1) seg AP || seg BQ,
(2) ∆APR ~ ∆RQB, and
(3) Find ∠ RQB if ∠ PAR = 35°
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm. 
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Practice Set 3.3 [Pages 63 - 64]
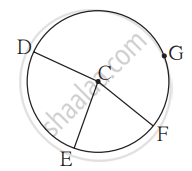
In the given figure, points G, D, E, and F are concyclic points of a circle with centre C. ∠ECF = 70°, m(arc DGF) = 200°. Find m(arc DE) and m(arc DEF).
In the given figure, ∆QRS is an equilateral triangle. Prove that,
- arc RS ≅ arc QS ≅ arc QR
- m(arc QRS) = 240°.

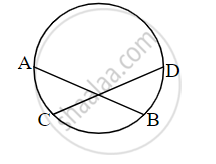
In the given figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Practice Set 3.4 [Pages 73 - 74]
In the given figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
(1) ∠ AOB (2)∠ ACB
(3) arc AB (4) arc ACB.
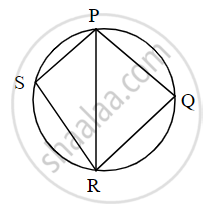
In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find -
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ
`square`MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N.
In the given figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠ RTS is an acute angle.
Prove that, any rectangle is a cyclic quadrilateral
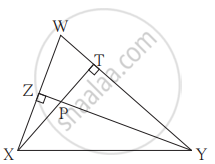
In the given figure, altitudes YZ and XT of ∆WXY intersect at P. Prove that,
- `square`WZPT is cyclic.
- Points X, Z, T, Y are concyclic.
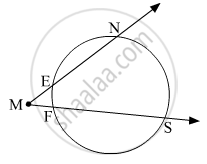
In the given figure, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠NMS.
In the given figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).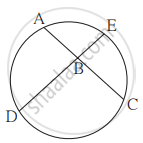
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Practice Set 3.5 [Page 82]
In the given figure, ray PQ touches the circle at point Q. PQ = 12, PR = 8, find PS and RS.
In the given figure, chord MN and chord RS intersect at point D.
(1) If RD = 15, DS = 4, MD = 8 find DN
(2) If RS = 18, MD = 9, DN = 8 find DS
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, if PQ = 6, QR = 10, PS = 8 find TS.
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2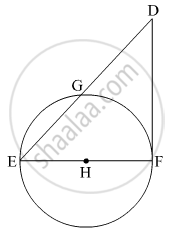
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 3 Circle Problem Set 3 [Pages 83 - 90]
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other. What is the distance between their centers ?
4.4 cm
8.8 cm
2.2 cm
8.8 or 2.2 cm
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles intersect each other such that each circle passes through the centre of the other. If the distance between their centres is 12, what is the radius of each circle?
6 cm
12 cm
24 cm
can’t say
Four alternative answers for the following question is given. Choose the correct alternative.
A circle touches all sides of a parallelogram. So the parallelogram must be a, ______
rectangle
rhombus
square
trapezium
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
25 cm
24 cm
7 cm
14 cm
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
One
Two
Three
Four
∠ACB is inscribed in arc ACB of a circle with centre O. If ∠ACB = 65°, find m(arc ACB).
65°
130°
295°
230°
Four alternative answers for the following question is given. Choose the correct alternative.
Chords AB and CD of a circle intersect inside the circle at point E. If AE = 5.6, EB = 10, CE = 8, find ED.
7
8
11.2
9
Four alternative answers for the following question is given. Choose the correct alternative
In a cyclic ▢ABCD, twice the measure of ∠A is thrice the measure of ∠C. Find the measure of ∠C?
36°
72°
90°
108°
Four alternative answers for the following question is given. Choose the correct alternative.
Points A, B, C are on a circle, such that m(arc AB) = m(arc BC) = 120°. No point, except point B, is common to the arcs. Which is the type of ∆ABC?
Equilateral triangle
Scalene triangle
Right angled triangle
Isosceles triangle
Four alternative answers for the following question is given. Choose the correct alternative.
Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true ? (i) It is not possible that ∠XYZ is an acute angle. (ii) ∠XYZ can’t be a right angle. (iii) ∠XYZ is an obtuse angle. (iv) Can’t make a definite statement for measure of ∠XYZ.
Only one
Only two
Only three
All
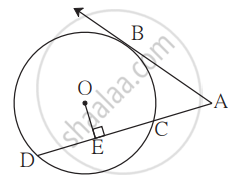
Line l touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.
- What is d(O, P) = ? Why?
- If d(O, Q) = 8 cm, where does the point Q lie?
- If d(O, Q) = 15 cm, How many locations of point Q are line on line l? At what distance will each of them be from point P?

In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 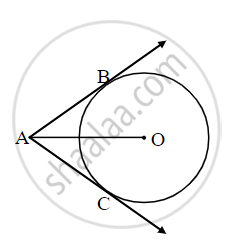
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

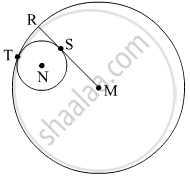
In the given figure, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions hence find the ratio MS:SR.
(1) Find the length of segment MT
(2) Find the length of seg MN
(3) Find the measure of ∠NSM.
In the adjoining figure circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill in the blanks and complete the proof.
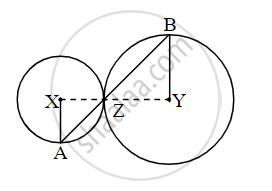
Construction: Draw segments XZ and YZ.
Proof:
By theorem of touching circles, points X, Z, Y are `square`.
∴ ∠XZA ≅ `square` ...(opposite angles)
Let ∠XZA = ∠BZY = a ...(I)
Now, seg XA ≅ seg XZ ...[Radii of the same circle]
∴∠XAZ = `square` = a ...[isosceles triangle theorem](II)
Similarly,
seg YB ≅ seg YZ ...[Radii of the same circle]
∴∠BZY = `square` = a ...[isosceles triangle theorem](III)
∴ from (I), (II), (III),
∠XAZ = `square`
∴ radius XA || radius YZ ...[`square`]
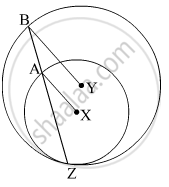
In the given figure, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger circle and it itersects smaller circle at point A. Prove that, seg AX || seg BY.
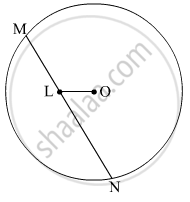
In the figure, line l touches the circle with center O at point P. Q is the midpoint of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12, find the radius of the circle.

In the given figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.

Draw circles with centres A, B and C each of radius 3 cm, such that each circle touches the other two circles.
Prove that any three points on a circle cannot be collinear.
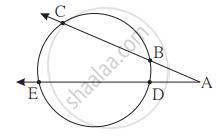
In the given figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
(1) What is the sum of ∠ TAQ and ∠ TSQ ?
(2) Find the angles which are congruent to ∠ AQP.
(3) Which angles are congruent to ∠ QTS ?
(4) ∠TAS = 65°, find the measure of ∠TQS and arc TS.
(5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.

In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

In the given figure, m(arc WY) = 44°, m(arc ZX) = 68°, then
(1) Find the measure of ∠ ZTX.
(2) If WT = 4.8, TX = 8.0,
YT = 6.4, find TZ.
(3) If WX = 25, YT = 8,
YZ = 26, find WT.

In the given figure,
(1) m(arc CE) = 54°, m(arc BD) = 23°, find measure of ∠CAE.
(2) If AB = 4.2, BC = 5.4, AE = 12.0, find AD.
(3) If AB = 3.6, AC = 9.0, AD = 5.4, find AE.
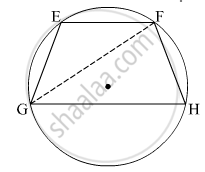
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.
In the given figure, P is the point of contact.
(1) If m(arc PR) = 140°, ∠ POR = 36°, find m(arc PQ)
(2) If OP = 7.2, OQ = 3.2, find OR and QR
(3) If OP = 7.2, OR = 16.2, find QR.

In the given figure, circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.

In the given figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD.
Complete the following proof by filling in the blanks.
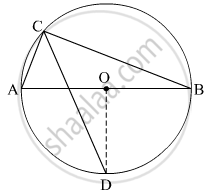
Proof: Draw seg OD.
∠ACB = ______ ...(Angle inscribed in semicircle)
∠DCB = ______ ...(CD is the bisector of ∠C)
m(arc DB) = ______ ...(Inscribed angle theorem)
∠DOB = ______ ...(Definition of measure of an arc)(I)
seg OA ≅ seg OB ...( ____________ )(II)
∴ line OD is ______ of seg AB. ...[From (I) and (II)]
∴ seg AD ≅ seg BD.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
In the given figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.
Prove that, ∠ PRQ + ∠ PSQ = 180°
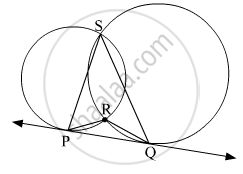
In the given figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.

In the given figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that ▢ABCD is cyclic.
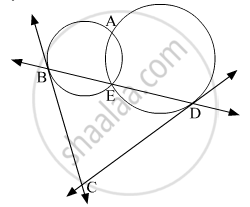
In the given figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Ponit O is the orthocentre. Prove that , point O is the incentre of ∆DEF.

Solutions for 3: Circle
Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board chapter 3 - Circle
Shaalaa.com has the Maharashtra State Board Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board Maharashtra State Board solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Balbharati solutions for Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board Maharashtra State Board 3 (Circle) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Balbharati textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board chapter 3 Circle are Circles Passing Through One, Two, Three Points, Converse of Tangent Theorem, Tangent Segment Theorem, Inscribed Angle Theorem, Corollaries of Inscribed Angle Theorem, Theorem: Opposite angles of a cyclic quadrilateral are supplementary., Corollary of Cyclic Quadrilateral Theorem, Converse: If a Pair of Opposite Angles of a Quadrilateral is Supplementary, Then the Quadrilateral is Cyclic., Theorem of Angle Between Tangent and Secant, Converse of Theorem of the Angle Between Tangent and Secant, Theorem of Internal Division of Chords, Theorem of External Division of Chords, Tangent to a Circle, Number of Tangents from a Point on a Circle, Touching Circles, Concept of Circle, Secant and Tangent, Theorem of Touching Circles, Tangent Properties - If Two Circles Touch, the Point of Contact Lies on the Straight Line Joining Their Centers, Introduction to an Arc, Congruence of Arcs, Property of Sum of Measures of Arcs, Inscribed Angle, Intercepted Arc, Cyclic Quadrilateral, Converse of Cyclic Quadrilateral Theorem, Tangent Secant Segments Theorem, Tangent - Secant Theorem, Angle Subtended by the Arc to the Point on the Circle, Angle Subtended by the Arc to the Centre.
Using Balbharati Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board solutions Circle exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Balbharati Solutions are essential questions that can be asked in the final exam. Maximum Maharashtra State Board Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board students prefer Balbharati Textbook Solutions to score more in exams.
Get the free view of Chapter 3, Circle Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board additional questions for Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board Maharashtra State Board, and you can use Shaalaa.com to keep it handy for your exam preparation.
![Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board chapter 3 - Circle Balbharati solutions for Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board chapter 3 - Circle - Shaalaa.com](/images/geometry-mathematics-2-english-10-standard-ssc-maharashtra-state-board_6:e2c9bb85175b46e28111cc27e179e2ce.png)
