Advertisements
Advertisements
प्रश्न
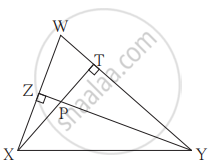
In the given figure, altitudes YZ and XT of ∆WXY intersect at P. Prove that,
- `square`WZPT is cyclic.
- Points X, Z, T, Y are concyclic.
उत्तर
(1) ∠WZP = ∠WTP = 90°
∴ ∠WZP + ∠WTP = 90° + 90° = 180°
∴ by converse of cyclic quadrilateral theorem,
`square`WZPT is cyclic.
(2) ∠XZY = ∠XTY = 90° ...(Given)
∴ points X and Y on line XY subtend equal angles at two distinct points Z and T on the same side of line XY.
If two points on a given line subtend equal angles at two distinct points that lie on the same side of the line, then the four points are concyclic.
∴ Points X, Z, T, Y are concyclic.
संबंधित प्रश्न
In the following figure, O is the centre of the circle. ∠ABC is inscribed in arc ABC and ∠ ABC = 65°. Complete the following activity to find the measure of ∠AOC.
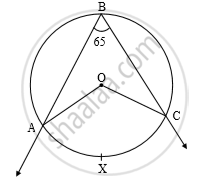
∠ABC = `1/2`m ______ (Inscribed angle theorem)
______ × 2 = m(arc AXC)
m(arc AXC) = _______
∠AOC = m(arc AXC) (Definition of measure of an arc)
∠AOC = ______

In the above figure, ∠ABC is inscribed in arc ABC.
If ∠ABC = 60°. find m ∠AOC.
Solution:
∠ABC = `1/2` m(arc AXC) ......`square`
60° = `1/2` m(arc AXC)
`square` = m(arc AXC)
But m ∠AOC = \[\boxed{m(arc ....)}\] ......(Property of central angle)
∴ m ∠AOC = `square`
