Advertisements
Advertisements
प्रश्न
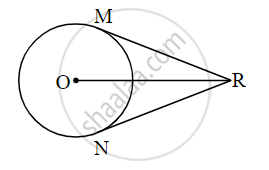
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
- What is the length of each tangent segment?
- What is the measure of ∠MRO?
- What is the measure of ∠MRN?

उत्तर
(1) It is given that seg RM and seg RN are tangent segments touching the circle at M and N, respectively.
∴ ∠OMR = ∠ONR = 90º ...(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

OM = 5 cm and OR = 10 cm
In right ∆OMR,
OR2 = OM2 + MR2
MR = `sqrt("OR"^2 - "OM"^2`
MR = `sqrt(10^2 - 5^2)`
MR = `sqrt(100 - 25)`
MR = `sqrt75`
MR = 5`sqrt3` cm
Tangent segments drawn from an external point to a circle are congruent.
∴ MR = NR = 5`sqrt3`
(2) In right ∆OMR,
∠MRO = `"OM"/"MR"`
∠MRO = `(5 "cm")/(5sqrt3cm)`
= `1/sqrt3`
∠MRO = tan 30°
∠MRO = 30°
Thus, the measure of ∠MRO is 30º.
Similarly, ∠NRO = 30º
(3) ∠MRN = ∠MRO + ∠NRO = 30º + 30º = 60º
Thus, the measure of ∠MRN is 60º.
संबंधित प्रश्न
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm. 
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
Four alternative answers for the following question is given. Choose the correct alternative.
Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true ? (i) It is not possible that ∠XYZ is an acute angle. (ii) ∠XYZ can’t be a right angle. (iii) ∠XYZ is an obtuse angle. (iv) Can’t make a definite statement for measure of ∠XYZ.
In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Segment DP and segment DQ are tangent segments to the circle with center A. If DP = 7 cm. So find the length of the segment DQ.
The chords corresponding to congruent arcs of a circle are congruent. Prove the theorem by completing following activity.
Given: In a circle with centre B
arc APC ≅ arc DQE
To Prove: Chord AC ≅ chord DE
Proof: In ΔABC and ΔDBE,
side AB ≅ side DB ......`square`
side BC ≅ side `square` .....`square`
∠ABC ≅ ∠DBE ......[Measure of congruent arcs]
∆ABC ≅ ∆DBE ......`square`
Length of a tangent segment drawn from a point which is at a distance 15 cm from the centre of a circle is 12 cm, find the diameter of the circle?
In the adjoining figure, O is the center of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
(i) What is the length of each tangent segment?
(ii) What is the measure of ∠MRO?
(iii) What is the measure of ∠MRN?
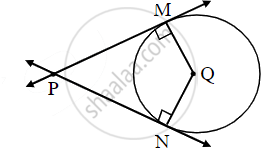
In the adjoining figure circle with Centre, Q touches the sides of ∠MPN at M and N. If ∠MPN = 40°, find measure of ∠MQN.
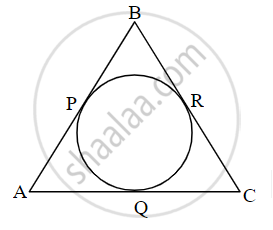
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
In a parallelogram ABCD, ∠B = 105°. Determine the measure of ∠A and ∠D.
In the following figure, XY = 10 cm and LT = 4 cm. Find the length of XT.
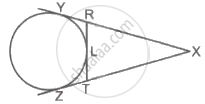

A circle touches side BC at point P of the ΔABC, from outside of the triangle. Further extended lines AC and AB are tangents to the circle at N and M respectively. Prove that : AM = `1/2` (Perimeter of ΔABC)
