Advertisements
Advertisements
प्रश्न
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
उत्तर
Let the radius of the base of the cone be r cm.
Height of the cone, h = 12 cm
The slant height of the cone, l = 13 cm
Now,
`"r"^2 +"h"^2 = "l"^2`
⇒ `"r"^2 + (12)^2 = (13)^2`
⇒ `"r"^2 + 144 = 169`
⇒ `"r"^2 = 169 - 144 = 25`
⇒ `"r" = sqrt(25) = 5 "cm"`
Thus, the radius of the base of the cone is 5 cm.
APPEARS IN
संबंधित प्रश्न
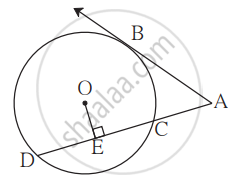
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2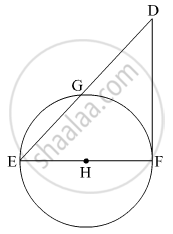
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
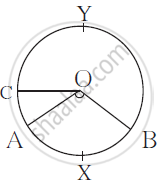
In the following figure ‘O’ is the centre of the circle.
∠AOB = 1100, m(arc AC) = 450.
Use the information and fill in the boxes with proper numbers.
(i) m(arcAXB) =
(ii)m(arcCAB) =
(iv)∠COB =
(iv)m(arcAYB) =
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Length of a tangent segment drawn from a point which is at a distance 15 cm from the centre of a circle is 12 cm, find the diameter of the circle?
Tangent segments drawn from an external point to a circle are congruent, prove this theorem. Complete the following activity.
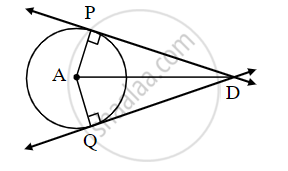
Given: `square`
To Prove: `square`
Proof: Draw radius AP and radius AQ and complete the following proof of the theorem.
In ∆PAD and ∆QAD,
seg PA ≅ `square` .....[Radii of the same circle]
seg AD ≅ seg AD ......[`square`]
∠APD ≅ ∠AQD = 90° .....[Tangent theorem]
∴ ∆PAD ≅ ∆QAD ....[`square`]
∴ seg DP ≅ seg DQ .....[`square`]
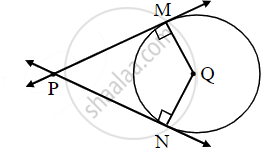
In the adjoining figure circle with Centre, Q touches the sides of ∠MPN at M and N. If ∠MPN = 40°, find measure of ∠MQN.
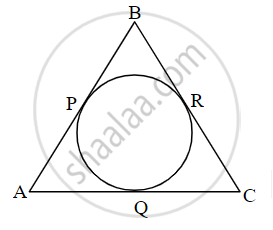
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
Prove that, tangent segments drawn from an external point to the circle are congruent.
In a parallelogram ABCD, ∠B = 105°. Determine the measure of ∠A and ∠D.
In the following figure, XY = 10 cm and LT = 4 cm. Find the length of XT.
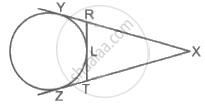

A circle touches side BC at point P of the ΔABC, from outside of the triangle. Further extended lines AC and AB are tangents to the circle at N and M respectively. Prove that : AM = `1/2` (Perimeter of ΔABC)
