Advertisements
Advertisements
प्रश्न
In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
उत्तर १
(1)
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠MLK = 90º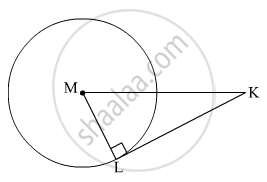
In right ∆MLK,
\[{MK}^2 = {ML}^2 + {LK}^2 \]
\[ \Rightarrow ML = \sqrt{{MK}^2 - {LK}^2}\]
\[ \Rightarrow ML = \sqrt{\left( 12 \right)^2 - \left( 6\sqrt{3} \right)^2}\]
\[ \Rightarrow ML = \sqrt{144 - 108}\]
\[ \Rightarrow ML = \sqrt{36} = 6 \] units
Thus, the radius of the circle is 6 units.
(2)
In right ∆MLK,
\[\tan\angle K = \frac{ML}{KL}\]
\[ \Rightarrow \tan\angle K = \frac{6}{6\sqrt{3}} = \frac{1}{\sqrt{3}}\]
\[ \Rightarrow \tan\angle K = \tan30°\]
\[ \Rightarrow \angle K = 30°\]
Using angle sum property, we have
\[\angle K + \angle L + \angle M = 180^\circ\]
\[ \Rightarrow 30^\circ + 90^\circ + \angle M = 180^\circ\]
\[ \Rightarrow 120^\circ + \angle M = 180^\circ\]
\[ \Rightarrow \angle M = 180^\circ - 120^\circ = 60^\circ\]
Thus, the measures of ∠K and ∠M are 30º and 60º, respectively.
उत्तर २
(1)
The line KL is the tangent to the circle at point L and seg ML is the radius. ...[Given]
∴ ∠MLK = 90º .... (i) [Tangent theorem]

In right ∆MLK,
∠MLK=90°
\[{MK}^2 = {ML}^2 + {LK}^2 \] ...[Pythagoras theorem]
\[ \Rightarrow ML = \sqrt{{MK}^2 - {LK}^2}\]
\[ \Rightarrow ML = \sqrt{\left( 12 \right)^2 - \left( 6\sqrt{3} \right)^2}\]
\[ \Rightarrow ML = \sqrt{144 - 108}\]
\[ \Rightarrow ML = \sqrt{36} = 6 \] units. ...[Taking the square root of both sides]
Thus, the radius of the circle is 6 units.
(2)
In right ∆MLK,
\[\Rightarrow\mathrm{ML = \frac{1}{2} MK}\]
∴ ∠K = 30° ...(ii) [Converse of 30° – 60° – 90° theorem]
In ∆MLK,
∠L = 90° ...[From (i)]
∠K = 30° ...[From (ii)]
∴ ∠M = 60° ...[Remaining angle of △MLK]
Thus, the measures of ∠K and ∠M are 30º and 60º, respectively.
संबंधित प्रश्न
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm. 
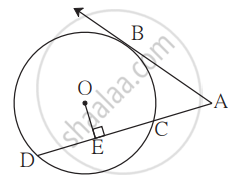
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2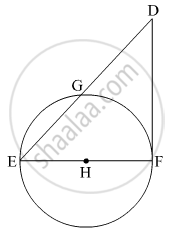
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
Four alternative answers for the following question is given. Choose the correct alternative.
Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true ? (i) It is not possible that ∠XYZ is an acute angle. (ii) ∠XYZ can’t be a right angle. (iii) ∠XYZ is an obtuse angle. (iv) Can’t make a definite statement for measure of ∠XYZ.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 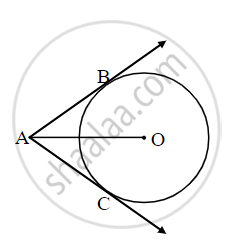
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
In the following figure ‘O’ is the centre of the circle.
∠AOB = 1100, m(arc AC) = 450.
Use the information and fill in the boxes with proper numbers.
(i) m(arcAXB) =
(ii)m(arcCAB) =
(iv)∠COB =
(iv)m(arcAYB) =
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
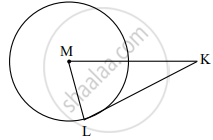
In the given figure, M is the centre of the circle and seg KL is a tangent segment. L is a point of contact. If MK = 12, KL = `6sqrt3`, then find the radius of the circle.
Segment DP and segment DQ are tangent segments to the circle with center A. If DP = 7 cm. So find the length of the segment DQ.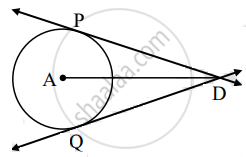
Length of a tangent segment drawn from a point which is at a distance 15 cm from the centre of a circle is 12 cm, find the diameter of the circle?
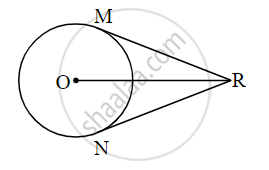
In the adjoining figure, O is the center of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
(i) What is the length of each tangent segment?
(ii) What is the measure of ∠MRO?
(iii) What is the measure of ∠MRN?
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
If AB and CD are the common tangents in the circles of two unequal (different) radii, then show that seg AB ≅ seg CD.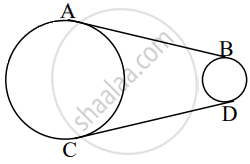
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.

Proof: In ∆RMO and ∆RNO,
∠RMO ≅ ∠RNO = 90° ......[`square`]
hypt OR ≅ hypt OR ......[`square`]
seg OM ≅ seg `square` ......[Radii of the same circle]
∴ ∆RMO ≅ ∆RNO ......[`square`]
∠MOR ≅ ∠NOR
Similairy ∠MRO ≅ `square` ......[`square`]
Prove that, tangent segments drawn from an external point to the circle are congruent.
