Advertisements
Advertisements
प्रश्न
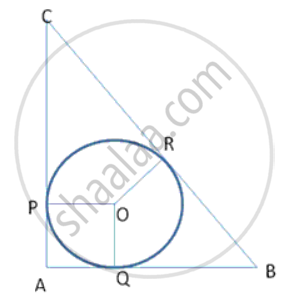
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
उत्तर
(1) It is given that line AB is tangent to the circle at A.
∴ ∠CAB = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
Thus, the measure of ∠CAB is 90º. 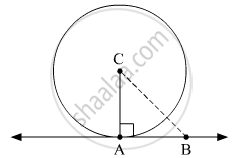
(2) Distance of point C from AB = 6 cm (Radius of the circle)
(3) ∆ABC is a right triangle.
CA = 6 cm and AB = 6 cm
Using Pythagoras theorem, we have
\[{BC}^2 = {AB}^2 + {CA}^2 \]
\[ \Rightarrow BC = \sqrt{6^2 + 6^2} \]
\[ \Rightarrow BC = 6\sqrt{2} cm\]
Thus, d(B, C) = \[6\sqrt{2}\]
(4) In right ∆ABC, AB = CA = 6 cm
∴ ∠ACB = ∠ABC (Equal sides have equal angles opposite to them)
Also, ∠ACB + ∠ABC = 90º (Using angle sum property of triangle)
∴ 2∠ABC = 90º
⇒ ∠ABC = \[\frac{90^\circ}{2}\]
Thus, the measure of ∠ABC is 45º.
APPEARS IN
संबंधित प्रश्न
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

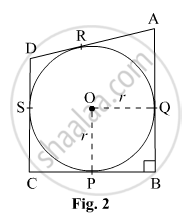
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
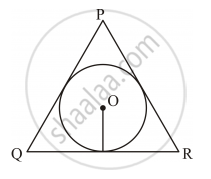
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
How many common tangents can be drawn to two circles, touching each
other externally?
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
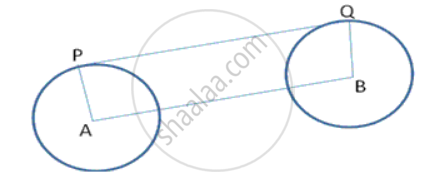
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
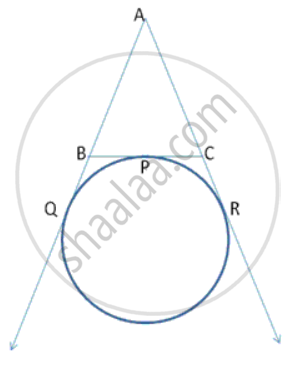
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
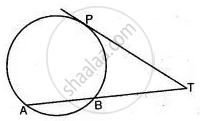
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
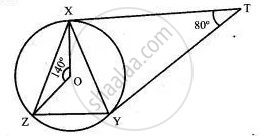
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
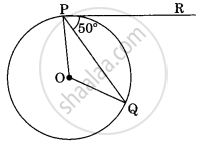
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
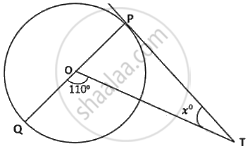
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.