Advertisements
Advertisements
प्रश्न
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
उत्तर
ABCD is a square whose diagonals AC and BD intersect each other at right angles at O.
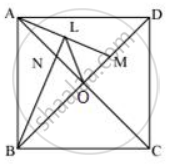
∠ BAM = ∠ BAO + ∠ OAM
⇒ ∠ BAM = `45° + (45°)/2 = 67 (1°)/2`
And
⇒ ∠ BMA = 180° - (∠ AOM + ∠ OAM)
⇒ ∠ BMA = 180° - 90° - `(45°)/2 = 90° - (45°)/2 = 67(1°)/2`
∴ ∠ BAM = ∠ BMA
APPEARS IN
संबंधित प्रश्न
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
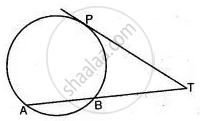
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
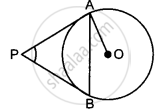
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
