Advertisements
Advertisements
प्रश्न
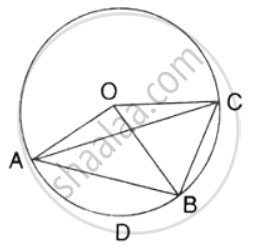
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
उत्तर
ABCD is a square whose diagonals AC and BD intersect each other at right angles at O.
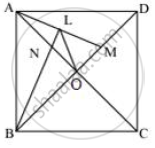
i. ∴ ∠AOB = ∠AOD = 90°
In ΔANB,
∠ANB = 180° – (∠NAB + ∠NBA)
`=>` `∠ANB = 180^circ - (45^circ + (45^circ)/2)` ...(NB is bisector of ∠ABD)
`=> ∠ANB = 180^circ - 45^circ - 45^circ/2 = 135^circ - 45^circ/2`
But, ∠LNO = ∠ANB ...(Vertically opposite angles)
∴ `∠LNO = 135^circ - 45^circ/2` ...(i)
Now in ΔAMO,
∠AMO = 180° – (∠AOM + ∠OAM)
`=> ∠AMO = 180^circ - (90^circ + (45^circ)/2)` ...(MA is bisector of ∠DAO)
`=>∠AMO = 180^circ - 90^circ - (45^circ)/2 = 90^circ - (45^circ)/2` ...(ii)
Adding (i) and (ii)
`∠LNO + ∠AMO = 135^circ - 45^circ/2 + 90^circ - 45^circ/2`
`=>` ∠LNO + ∠AMO = 225° – 45° = 180°
`=>` ∠ONL + ∠OML = 180°
ii. ∠BAM = ∠BAO + ∠OAM
`=> ∠BAM = 45^circ + (45^circ)/2 = 67 1^circ/2`
And
`=>` ∠BMA = 180° – (∠AOM + ∠OAM)
`=> ∠BMA = 180^circ - 90^circ - 45^circ/2`
= `90^circ - 45^circ/2`
= `67 1^circ/2`
∴ ∠BAM = ∠BMA
iii. In quadrilateral ALOB,
∵ ∠ABO + ∠ALO = 45° + 90° + 45° = 180°
Therefore, ALOB is a cyclic quadrilateral.
APPEARS IN
संबंधित प्रश्न
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

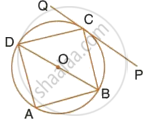
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.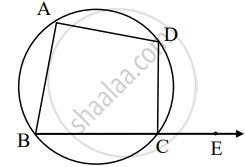
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
