Advertisements
Advertisements
प्रश्न
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
उत्तर

m ∠ A = 3 (m ∠C)
∠ A + ∠ C = 180 (Opposite angles of a cyclic quadrilateral)
3∠C + ∠ C = 180
4 ∠ C = 180
∠ C = 45
m ∠ A = 3 (m ∠ C)
= 3 × 45
= 135
m ∠ A = 135°
APPEARS IN
संबंधित प्रश्न
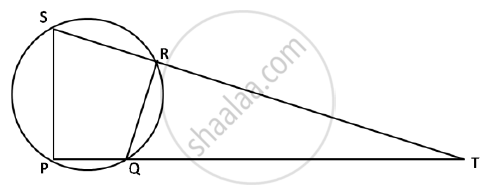
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
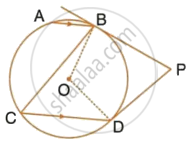
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.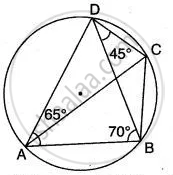
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.