Advertisements
Advertisements
प्रश्न
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

उत्तर
We know that angle by the same arc at circle i.e., on the circumference is half of the angle by the same arc at the center.
∵ ∠x = `1/2` x 160° = 80° ....(Opposite triangles of a cyclic quadrilateral supplementary)
∴ ∠x + ∠y = 180°
∴ ∠y = 100°
∴ 3∠y - 2∠x
= 3 x 100° - 2 x 80°
= 300° - 160°
= 140°.
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
Use the given figure to find:
- ∠BAD,
- ∠DQB.
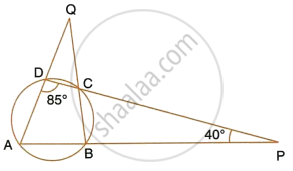
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
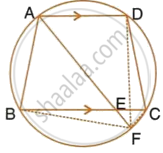
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In the figure, given below, find: ∠ABC. Show steps of your working.

The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
