Advertisements
Advertisements
प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

उत्तर

i. ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠BCD = 180° – 96° = 84°
∴ ∠BCE = 180° – 84° = 96°
Similarly, BCEF is a cyclic quadrilateral
∴ ∠BCE + ∠BFE = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
∴ ∠BFE = 180° – 96° = 84°
ii. Now, ∠BAD + ∠BFE
= 96° + 84°
= 180°
But these two are interior angles on the same side of a pair of lines AD and FE
∴ AD || FE
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

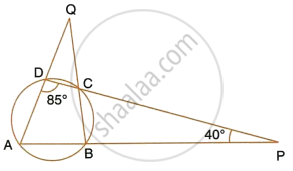
Use the given figure to find:
- ∠BAD,
- ∠DQB.
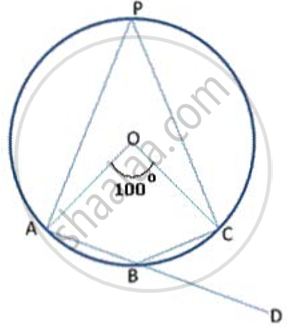
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
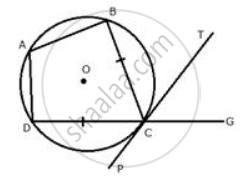
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In following fig., O is the centre of the circle. Find ∠ CBD.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
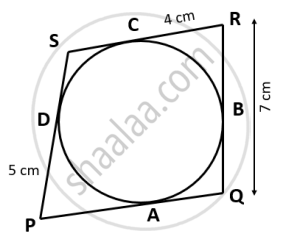
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: