Advertisements
Advertisements
प्रश्न
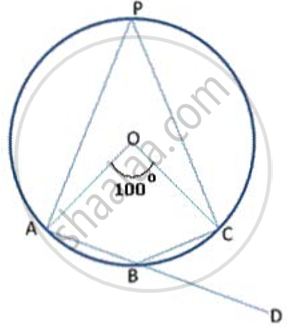
In following fig., O is the centre of the circle. Find ∠ CBD.
उत्तर
It is given that ∠ AOC = 100°
Arc AC subtends ∠ AOC at the centre of circle and ∠ APC on the circumference of the circle
∴ ∠ AOC = 2 c
⇒ ∠ APC = `(100°)/2` = 50°
It can be seen that APCB is a cyclic quadriIateral.
∴ ∠ APC + ∠ ABC = 180° (Sum of opposite angles of a cyclic quadrilateral)
⇒ ∠ ABC = 180° - 50° = 130°
Now , ∠ ABC + ∠ CBD = 180° (Linear pair angles)
∠ CBD = 180° - 130° = 50°
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

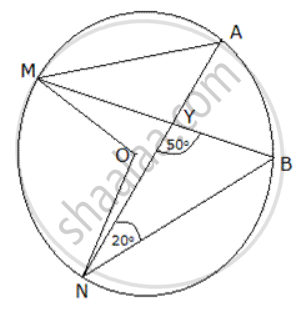
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
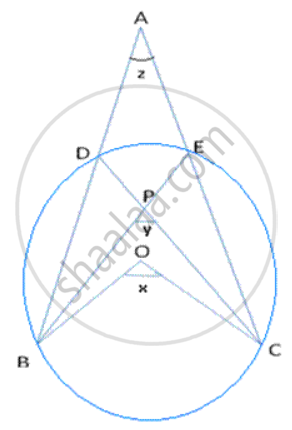
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
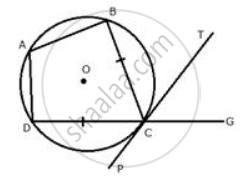
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
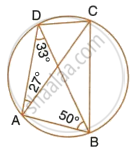
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.