Advertisements
Advertisements
प्रश्न
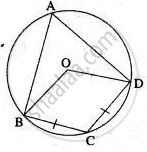
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

उत्तर
Given: PQRS is a cyclic quadrilateral.
∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°
1) Opposite angle of a cyclic quadrilateral is supplementary.
⇒ ∠QPS + ∠QRS = 180°
⇒ 73° + ∠QRS = 180°
⇒ ∠QRS = 180° - 73= 107°
2) Opposite angle of a cyclic quadrilateral are supplementary.
⇒ ∠PSR + ∠PQR = 180°
⇒ ∠PSR + (⇒ ∠PQS + ⇒ ∠RQS) = 180°
⇒ 82° + 55° + ∠RQS = 180°
⇒ ∠RQS = 180° - 137° = 43°
3) In ΔPQS, by angle sum property, we have
⇒ ∠PSQ + ∠PQS + ∠QPS = 180°
⇒ ∠PSQ + 55° + 73° = 180°
⇒ ∠PSQ = 180° - 128° = 52°
Now ⇒ ∠PRQ = ∠PSQ (angles in the same segment of a circle)
⇒ ∠PRQ = 52°
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.