Advertisements
Advertisements
प्रश्न
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
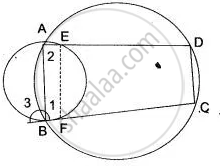
उत्तर
In order to prove that EF || DC. It is sufficient to show that ∠2 = ∠3.
Since ABCD is a cyclic quadrilateral.
∴ ∠1 + ∠3 = 180° ...(i)
Similarly, in the cyclic quadrilateral ABFE, we have
∠1 + ∠2 = 180° ...(ii)
From (i) and (ii), we get
⇒ ∠1 + ∠3 = ∠1 + ∠2
⇒ ∠3 = ∠2
Hence, EF || DC.
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
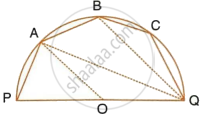
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
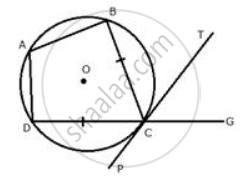
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the following figure, O is the centre of the circle. Find the values of a, b and c.
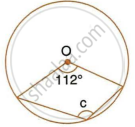
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
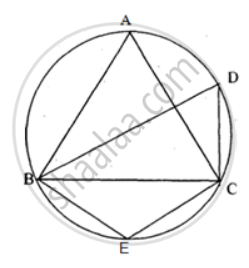
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
