Advertisements
Advertisements
प्रश्न
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
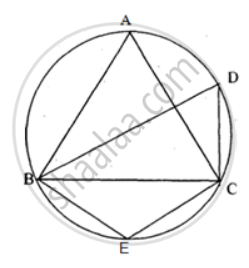
उत्तर
In cyclic quadrialteral ABEC,
∠BAC + ∠BEC = 180°
⇒ ∠BAC + 148° = 180°
⇒ ∠BAC = 180° - 148°
⇒ ∠BAC = 32°
APPEARS IN
संबंधित प्रश्न
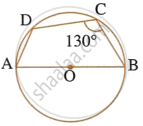
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
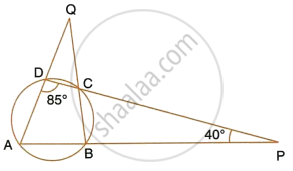
Use the given figure to find:
- ∠BAD,
- ∠DQB.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the figure, given below, find: ∠ABC. Show steps of your working.

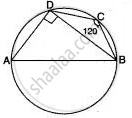
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
If O is the centre of the circle, find the value of x in each of the following figures
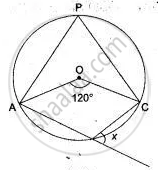
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA