Advertisements
Advertisements
प्रश्न
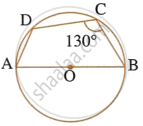
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
उत्तर
i. ∠DAB + ∠BCD = 180° ...(Opposite angle of a cyclic quadrilateral)
∠DAB + 130° = 180°
∠DAB = 180° – 130°
∠DAB = 50°
ii. ∠ADB = 90° ...(Angle in semicircle)
In ΔADB,
∠DAB + ∠ADB + ∠DBA = 180° ...(Angle sum property)
50° + 90° + ∠DBA = 180°
∠DBA = 180° – 140°
∠DBA = 40°
APPEARS IN
संबंधित प्रश्न
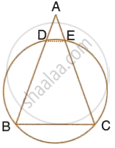
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
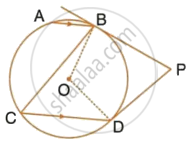
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
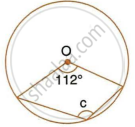
In the following figure, O is the centre of the circle. Find the values of a, b and c.
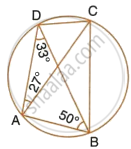
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
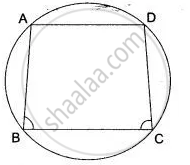
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
