Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
उत्तर
QC is tangent to the circle
∴ ∠ CAB = ∠ QCB
Angle between tangent and chord = angle in alternate segment
∴ ∠ QCB = 34°
ABQ is a straight line
⇒ ∠ ABC + ∠ CBQ = 180°
⇒ 56° + ∠ CBQ = 180°
⇒ CBQ = 124°
Now,
∠ CQB = 180° - ∠ QCB = CBQ
⇒ ∠ CQB = 180° - 34°- 124°
⇒ ∠ CQB = 22°
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
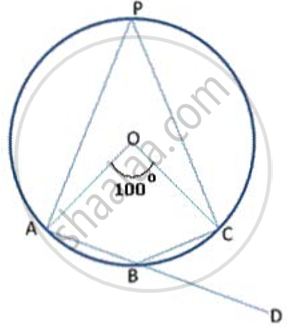
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
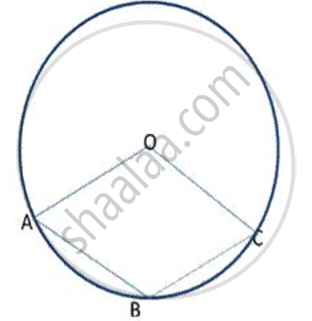
In following fig., O is the centre of the circle. Find ∠ CBD.
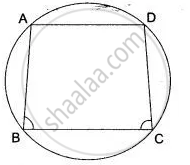
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
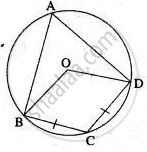
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
