Advertisements
Advertisements
Question
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
Solution
QC is tangent to the circle
∴ ∠ CAB = ∠ QCB
Angle between tangent and chord = angle in alternate segment
∴ ∠ QCB = 34°
ABQ is a straight line
⇒ ∠ ABC + ∠ CBQ = 180°
⇒ 56° + ∠ CBQ = 180°
⇒ CBQ = 124°
Now,
∠ CQB = 180° - ∠ QCB = CBQ
⇒ ∠ CQB = 180° - 34°- 124°
⇒ ∠ CQB = 22°
APPEARS IN
RELATED QUESTIONS
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
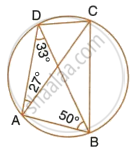
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
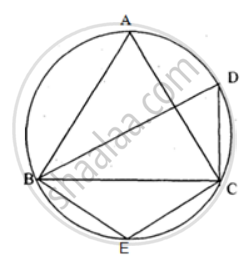
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
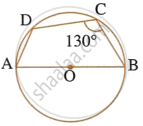
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
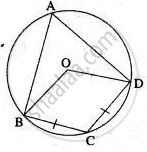
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

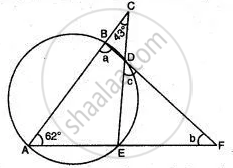
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.