Advertisements
Advertisements
Question
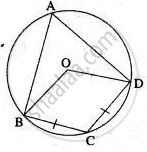
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
Solution
(i) ∠ BOD = 2 x ∠ BAD = 2 x 75° = 150°
∠ BOC = ∠ COD
∵ BC = CD
∴ ∠ BOD = 2 ∠ BOC
∴ ∠ BOC = `1/2` ∠ BOD = 75°
(ii) ∠ OBD = `1/2`( 180° - ∠ BOD)
∠ OBD = `1/2`( 180° - 150°) = 15°
(iii) ∠ BCD = 180° - ∠ BAD ....(Opposite ∠S of a cyclic quadrilateral is supplementary.)
∠ BCD = 180° - 75°
∠ BCD = 105°
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
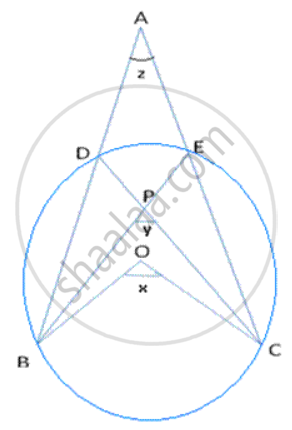
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
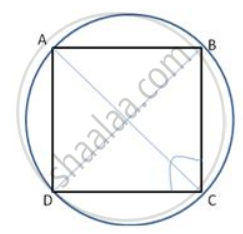
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
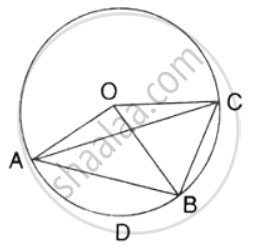
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
