Advertisements
Advertisements
Question
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
Solution 1
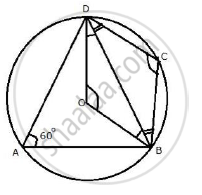
∠ BOD = 2 ∠BAD = 2 × 60° = 120°
And ∠ BCD = `1/2` Refelx (∠BOD) ( 360° - 120°) = 120°
(Angle at the centre is double the angle at the circumference subtended by the same chord
∴ ∠CBD + ∠CDB =180° - 120° = 60°
(By angle sum property of triangle CBD)
Again, ∠OBD+ ∠ODB=180° - 120° = 60°
(By angle sum property of triangle OBD)
∴ ∠OBD + ∠ODB = ∠CBD+ ∠CDB
Solution 2
Here, ∠ BOD = 2 ∠BAD = 2 × 60° = 120°.
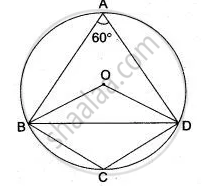
Now in Δ BOD,
∠OBD + ∠ODB = 180° - 120° = 60° ....(i)
Also, ∠DAB + ∠DCB = 180° ...(ABCD is cyclic quadrilateral)
∠DCB = 180° - 60° = 120° ...(ii)
∴ In Δ BCD,
∠ CBD + ∠CDB = 180° - ∠DCB = 180° - 120° = 60°
from (i) and (ii), we get the required result.
∴ ∠OBD + ∠ODB = ∠CBD+ ∠CDB.
Hence proved.
APPEARS IN
RELATED QUESTIONS
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
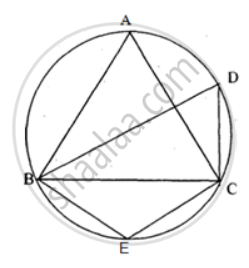
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.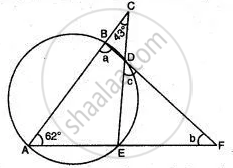
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.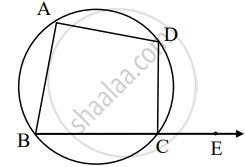
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
