Advertisements
Advertisements
Question
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

Solution

i. ∠DBC = ∠DAC = 27°
(Angle subtended by the same chord on the circle are equal)
ii. ∠ACB = ∠ADB = 33°
∠ACD = ∠ABD = 50°
(Angle subtended by the same chord on the circle are equal)
∴ ∠DCB = ∠ACD + ∠ACB
= 50° + 33°
= 83°
iii. ∠DAB + ∠DCB = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 27° + ∠CAB + ∠83° = 180°
`=>` ∠CAB = 180° – 110° = 70°
APPEARS IN
RELATED QUESTIONS
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
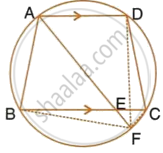
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
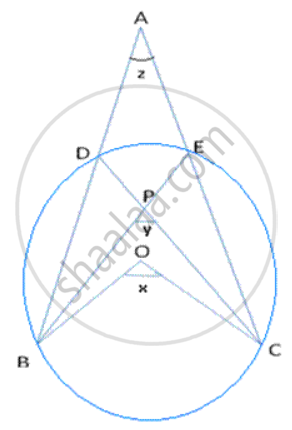
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
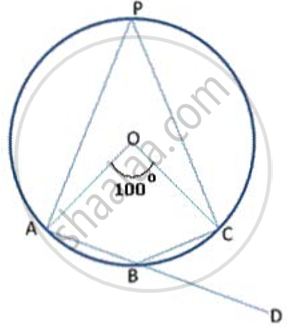
In following fig., O is the centre of the circle. Find ∠ CBD.
In the following figure, Prove that AD is parallel to FE.

