Advertisements
Advertisements
Question
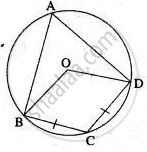
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
Solution
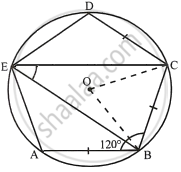
i. Join OC and OB.
AB = BC = CD and ∠ABC = 120°
∴ ∠BCD = ∠ABC = 120°
OB and OC are the bisectors of ∠ABC and ∠BCD respectively.
∴ ∠OBC = ∠BCO = 60°
In ΔBOC,
∠BOC = 180° – (∠OBC + ∠BOC)
`=>` ∠BOC = 180° – (60° + 60°)
`=>` ∠BOC = 180° – 120° = 60°
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∴ `∠BEC = 1/2 ∠BOC = 1/2 xx 60^circ = 30^circ`
ii. In cyclic quadrilateral BCDE,
∠BED + ∠BCD = 180°
`=>` ∠BED + 120° = 180°
∴ ∠BED = 180° – 120° = 60°
APPEARS IN
RELATED QUESTIONS
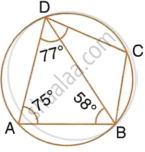
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
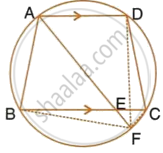
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
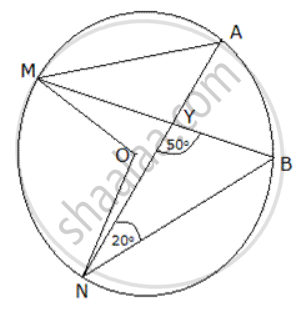
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
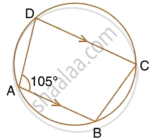
In the figure, given below, find: ∠ADC, Show steps of your working.
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.