Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Solution
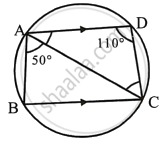
ABCD is a cyclic quadrilateral in which AD || BC
∠ADC = 110°, ∠BAC = 50°
∠B + ∠D = 180°
(Sum of opposite angles of a quadrilateral)
`=>` ∠B + 110° = 180°
`=>` ∠B = 70°
Now in ΔABC,
∠BAC + ∠ABC + ∠ACB = 180°
`=>` 50° + 70° + ∠ACB = 180°
`=>` ∠ACB = 180° – 120° = 60°
∵ AD || BC
∴ ∠DAC = ∠ACB = 60° ...(Alternate angles)
Now in ΔADC,
∠DAC + ∠ADC + ∠DCA = 180°
`=>` 60° + 110° + ∠DCA = 180°
`=>` ∠DCA = 180° – 170° = 10°
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.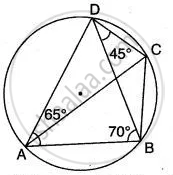
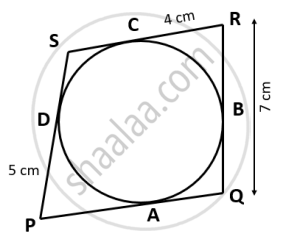
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: