Advertisements
Advertisements
Question
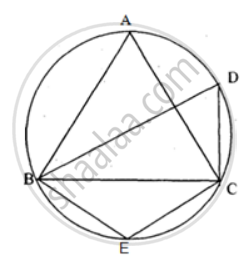
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
Solution
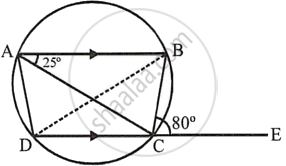
In the given figure,
ABCD is a cyclic quad in which AB || DC
∴ ABCD is an isosceles trapezium
∴ AD = BC
i. Join BD
Ext. ∠BCE = ∠BAD ...[Exterior angle of a cyclic qud is equal to interior opposite angle]
∴ ∠BAD = 80° ...[∵ ∠BCE = 80°]
But ∠BAC = 25°
∴ ∠CAD = ∠BAD – ∠BAC
= 80° – 25°
= 55°
ii. ∠CBD = ∠CAD ...[Angle of the same segment]
= 55°
iii. ∠ADC = ∠BCD ...[Angles of the isosceles trapezium]
= 180° – ∠BCE
= 180° – 80°
= 100°
APPEARS IN
RELATED QUESTIONS
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
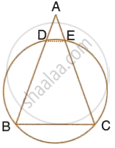
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
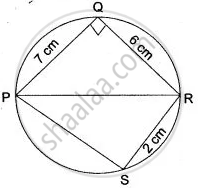
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.