Advertisements
Advertisements
प्रश्न
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
उत्तर
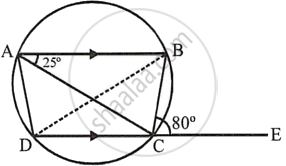
In the given figure,
ABCD is a cyclic quad in which AB || DC
∴ ABCD is an isosceles trapezium
∴ AD = BC
i. Join BD
Ext. ∠BCE = ∠BAD ...[Exterior angle of a cyclic qud is equal to interior opposite angle]
∴ ∠BAD = 80° ...[∵ ∠BCE = 80°]
But ∠BAC = 25°
∴ ∠CAD = ∠BAD – ∠BAC
= 80° – 25°
= 55°
ii. ∠CBD = ∠CAD ...[Angle of the same segment]
= 55°
iii. ∠ADC = ∠BCD ...[Angles of the isosceles trapezium]
= 180° – ∠BCE
= 180° – 80°
= 100°
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

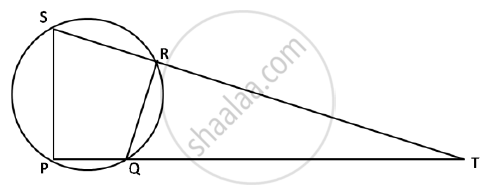
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
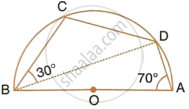
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
Use the given figure to find:
- ∠BAD,
- ∠DQB.
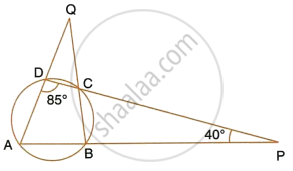
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
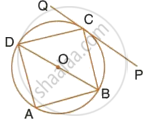
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

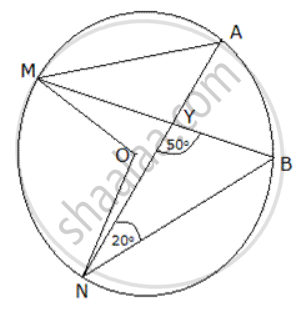
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC