Advertisements
Advertisements
प्रश्न
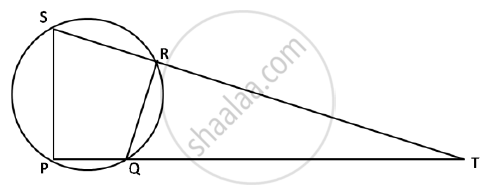
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
उत्तर
1) Since `square PQRS` is a cyclic quadrilateral
`angle QRT = angle SPT` ....(1)(exterior angle is equal to interior opposite angle)
In ΔTPS and ΔTRQ
`angle PTS = angle RTQ` . . . .(common angle)
`angleQRT = angle SPT` . . . .(from 1)
⇒ ΔTPS ~ ΔTRQ . . . .(AA similarity criterion)
2) Since ΔTPS ~ ΔTRQ, implies that corresponding sides are proportional
`i.e (SP)/(QR) = (TP)/(TR)`
`=> (SP)/4 = 18/6`
`=> (SP)= (18xx4)/6`
`=> SP = 12cm`
3) Since ΔTPS ~ ΔTRQ
`(Ar(ΔTPS))/(Ar(ΔTRQ)) = "SP"^2/"RQ"^2`
`=> 27/(Ar(ΔTRQ)) = (27xx4xx4)/(12xx12)`
`=> Ar(ΔTRQ) = 3cm^2`
Now, Ar(`square PQRS`) = Ar(ΔTPS) Ar(ΔTRQ)= 27 - 3 = 24 cm2
APPEARS IN
संबंधित प्रश्न
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
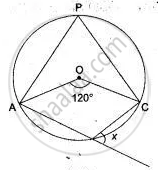
If O is the centre of the circle, find the value of x in each of the following figures